Normal Mapping
- 2.16.1. Overview
- 2.16.2. Tangent Space
- 2.16.3. Tangent/Bitangent Generation
- 2.16.4. Normal Maps
- 2.16.5. Rendering With Normal Maps
Overview
The io7m-r1 package
supports the use of tangent-space normal mapping
to allow for per-pixel control over the surface normal of rendered triangles.
This allows for meshes to appear to have very complex surface details without
requiring those details to actually be rendered as triangles within the scene.
Tangent Space
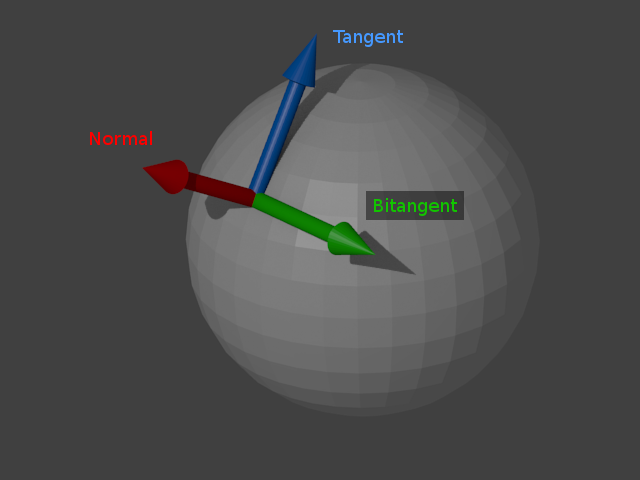
Conceptually, there is a three-dimensional coordinate system based
at each vertex, formed by three orthonormal basis vectors: The vertex normal,
tangent and bitangent
vectors. The normal vector is a the vector perpendicular
to the surface at that vertex. The tangent and
bitangent vectors are parallel to the surface, and
each vector is obviously perpendicular to the other two vectors. This coordinate
space is often referred to as tangent space. The
normal vector actually forms the
Z axis of the coordinate space, and this
fact is central to the process of normal mapping. The coordinate system at
each vertex may be left or right-handed depending on the arrangement of UV
coordinates at that vertex.
Tangent/Bitangent Generation
Tangent and bitangent
vectors can be generated by the modelling programs that artists use to
create polygon meshes, but, additionally, the
RMeshTangents
class can take an arbitrary mesh with only normal vectors and UV
coordinates and produce tangent and bitangent vectors. The full
description of the algorithm used is given in
Mathematics for 3D Game Programming and Computer Graphics, Third Edition
[30],
and also in an
article
by the same author. The actual aim of tangent/bitangent generation
is to produce a pair of orthogonal vectors that are oriented to the
x and y
axes of an arbitrary texture. In order to do achieve this,
the generated vectors are oriented according to the UV
coordinates in the mesh.
In the io7m-r1 package, the
bitangent vector is not actually stored in
the mesh data, and the tangent vector for
any given vertex is instead stored as a four-component vector.
The reasons for this are as follows: Because the normal, tangent, and
bitangent vectors are known to be orthonormal, it should be possible to
reconstruct any one of the three vectors given the other two at run-time.
This would eliminate the need to store one of the vectors and would
reduce the size of mesh data (including the on-disk size, and the
size of mesh data allocated on the GPU) by a significant amount.
Given any two orthogonal vectors V0
and V1, a vector orthogonal to both
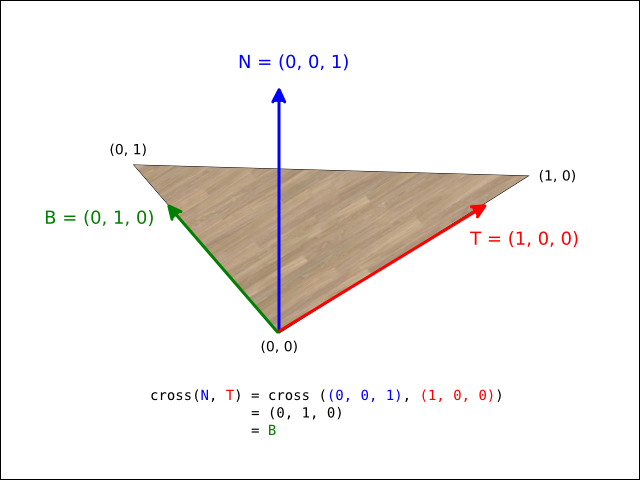
can be calculated by taking the cross product
of both, denoted (cross V0 V1). The
problem here is that if V0 is assumed
to be the original normal vector N,
and V1 is assumed to be the original
tangent vector T, there is no guarantee
that (cross N T) will produce a
vector equal to the original bitangent vector
B: There are two possible
choices of value for B that differ
only in the sign of their coordinate values.
As an example, a triangle that will produce T
and B vectors that form a right-handed
coordinate system with the normal vector N
(with UV coordinates indicated at each vertex):
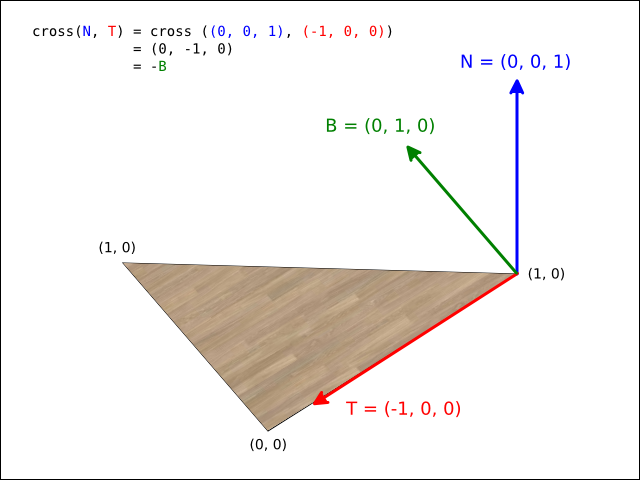
The same triangle will produce vectors that form a left-handed system when
generating vectors for another vertex (note that the result of
(Vector3f.cross N T) = (Vector3f.negation B)):
However, if the
original tangent vector T was augmented
with a piece of extra information that indicated whether or not the result of
(cross N T) needed to be inverted, then
reconstructing B would be trivial.
Therefore, the fourth component of the tangent vector T
contains 1.0 if
(cross N T) = B, and
-1.0 if (cross N T) = -B.
The bitangent vector can therefore be
reconstructed by calculating cross (N, T.xyz) * T.w.
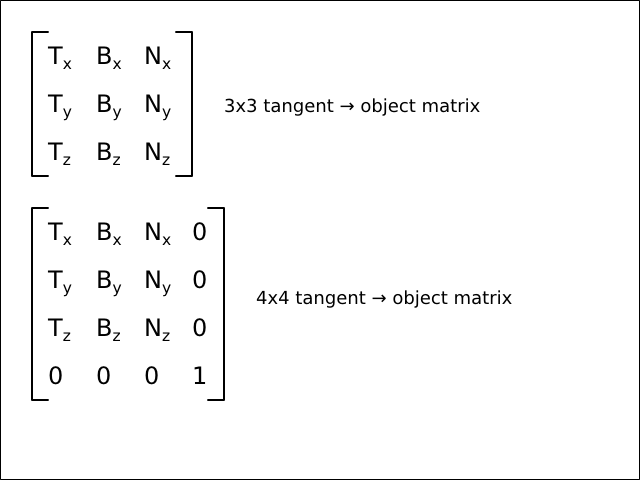
With the three vectors (T, B, N), it's now possible
construct a 3x3 matrix that can transform arbitrary
vectors in tangent space
to object space:
With this matrix, it's now obviously possible to take an arbitrary vector in
tangent space and transform it to object space. Then, with the
current normal matrix (object → eye),
transform the object space vector all the way to
eye space
in the same manner as ordinary per-vertex object space normal vectors.
Normal Maps
A normal map is an ordinary RGB texture
where each texel represents a tangent space normal vector. The
x coordinate is stored in the
red channel, the y coordinate is
stored in the green channel, and the z
coordinate is stored in the blue channel. The original
coordinate values are assumed to fall within the inclusive range
[-1.0, 1.0], and these values
are mapped to the range [0.0, 1.0]
before being encoded to a specific pixel format.
As an example, the vector (0.0, 0.0, 1.0)
is first mapped to (0.5, 0.5, 1.0) and
then, assuming an image format with 8-bits of precision per color channel,
encoded to (0x7f, 0x7f, 0xff). This
results in a pale blue color that is characteristic of tangent space
normal maps:
Typically, tangent space normal maps are generated from a simple
height maps: Greyscale images where 0.0
denotes the lowest possible height, and 1.0
indicates the highest possible height. There are multiple algorithms
that are capable of generating normal vectors from height maps, but
the majority of them work from the same basic principle: For a given
pixel with value h at location
(x, y) in an image, the neighbouring
pixel values at (x - 1, y),
(x - 1, y - 1),
(x + 1, y),
(x + 1, y + 1) are compared
with h
in order to determine the slope between
the height values. As an example, the
Prewitt (3x3) operator
when used from the
gimp-normalmap
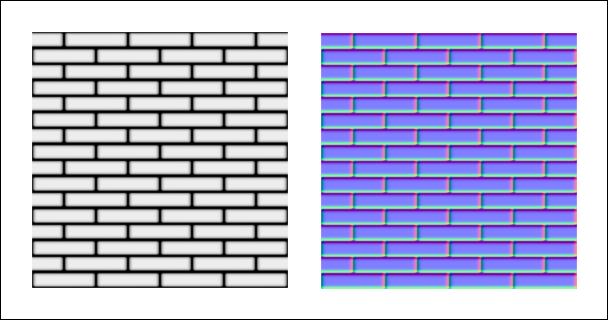
plugin will produce the following map from a given greyscale height map:
It is reasonably easy to infer the general directions of vectors from
a visual inspection of a tangent space normal map alone. In the above
image, the flat faces of the bricks are mostly pale blue. This is because the
tangent space normal for that surface is pointing straight towards the
viewer - mostly towards the positive z
direction. The right edges of the bricks in the image are tinted with a
pinkish hue - this indicates that the normal vectors at that pixel point
mostly towards the positive x direction.
Rendering With Normal Maps
As stated, the purpose of a normal map is to give per-pixel control
over the surface normal for a given triangle during rendering. The
process is as follows:
- Calculate the bitangent vector B from the N and T vectors. This step is performed on a per-vertex basis (in the vertex shader).
- Construct a 3x3 tangent → object matrix M from the (T, B, N) vectors. This step is performed on a per-fragment basis (in the fragment shader) using the interpolated vectors calculated in the previous step.
- Sample a tangent space normal vector P from the current normal map.
- Transform the vector P with the matrix M by calculating M * P, resulting in an object space normal vector Q.
- Transform the vector Q to eye space, in the same manner that an ordinary per-vertex normal vector would be (using the 3x3 normal matrix).
Effectively, a "replacement" normal vector is sampled from the
map, and transformed to object space using the existing
(T, B, N) vectors. When
the replacement normal vector is used when applying lighting,
the effect is dramatic. Given a simple two-polygon
square textured with the following albedo texture and normal map:
The square when textured and normal mapped, with three spherical
lights:
The same square with the same lights but missing the normal map:
[30]
See section 7.8.3, "Calculating tangent vectors".