Deferred Rendering: Position Reconstruction
- 2.21.1. Overview
- 2.21.2. Recovering Eye space Z
- 2.21.3. Recovering Eye space Z (Logarithmic depth encoding)
- 2.21.4. Recovering Eye space Z (Screen space depth encoding)
- 2.21.5. Recovering Eye space Position
- 2.21.6. Implementation
Overview
Applying lighting during deferred rendering is primarily a screen space technique. When the visible opaque objects have been rendered into the geometry buffer, the original eye space positions of all of the surfaces that resulted in visible fragments in the scene are lost (unless explicitly saved into the geometry buffer). However, given the knowledge of the projection that was used to render the scene (such as perspective or orthographic), it's possible to reconstruct the original eye space position of the surfaces that produced each of the fragments in the geometry buffer.
Specifically then, for each fragment f in the geometry buffer for which lighting is being applied, a position reconstruction algorithm attempts to reconstruct surface_eye - the eye space position of the surface that produced f - using the screen space position of the current light volume fragment position = (screen_x, screen_y) and some form of depth value (such as the screen space depth of f ).
Position reconstruction is a fundamental technique in deferred rendering, and there are a practically unlimited number of ways to reconstruct eye space positions for fragments, each with various advantages and disadvantages. Some rendering systems actually store the eye space position of each fragment in the geometry buffer, meaning that reconstructing positions means simply reading a value directly from a texture. Some systems store only a normalized eye space depth value in a separate texture: The first step of most position reconstruction algorithms is to compute the original eye space Z value of a fragment, so having this value computed during the population of the geometry buffer reduces the work performed later. Storing an entire eye space position into the geometry buffer is obviously the simplest and requires the least reconstruction work later on, but is costly in terms of memory bandwidth: Storing a full eye space position requires an extra 4 * 4 = 16 bytes of storage per fragment (four 32-bit floating point values). As screen resolutions increase, the costs can be prohibitive. Storing a normalized depth value requires only a single 32-bit floating point value per fragment but even this can be too much on less capable hardware. Some algorithms take advantage of the fact that most projections used to render scenes are perspective projections. Some naive algorithms use the full inverse of the current projection matrix to reconstruct eye space positions having already calculated clip space positions.
The algorithm that the r2 package uses for position reconstruction is generalized to handle both orthographic and perspective projections, and uses only the existing logarithmic depth values that were written to the depth buffer during scene rendering. This keeps the geometry buffer compact, and memory bandwidth requirements comparatively low. The algorithm works with symmetric and asymmetric viewing frustums, but will only work with near and far planes that are parallel to the screen.
The algorithm works in two steps: Firstly, the original eye space Z value of the fragment in question is recovered, and then this Z value is used to recover the full eye space position.
Recovering Eye space Z
During rendering of arbitrary scenes, vertices specified in object space are transformed to eye space, and the eye space coordinates are transformed to clip space with a projection matrix. The resulting 4D clip space coordinates are divided by their own w components, resulting in normalized-device space coordinates. These normalized-device space coordinates are then transformed to screen space by multiplying by the current viewport transform. The transitions from clip space to screen space are handled automatically by the graphics hardware.
The first step required is to recover the original eye space Z value of f. This involves sampling a depth value from the current depth buffer. Sampling from the depth buffer is achieved as with any other texture: A particular texel is addressed by using coordinates in the range [(0, 0), (1, 1)]. The r2 package currently assumes that the size of the viewport is the same as that of the framebuffer (width, height) and that the bottom left corner of the viewport is positioned at (0, 0) in screen space. Given the assumption on the position and size of the viewport, and assuming that the screen space position of the current light volume fragment being shaded is position = (screen_x, screen_y), the texture coordinates (screen_uv_x, screen_uv_y) used to access the current depth value are given by:
module ScreenToTexture where
import qualified Vector2f
screen_to_texture :: Vector2f.T -> Float -> Float -> Vector2f.T
screen_to_texture position width height =
let u = (Vector2f.x position) / width
v = (Vector2f.y position) / height
in Vector2f.V2 u v
Intuitively, (screen_uv_x, screen_uv_y) = (0, 0) when the current screen space position is the bottom-left corner of the screen, (screen_uv_x, screen_uv_y) = (1, 1) when the current screen space position is the top-right corner of the screen, and (screen_uv_x, screen_uv_y) = (0.5, 0.5) when the current screen space position is the exact center of the screen.
Originally, the spiritual ancestor of the r2 package, r1, used a standard depth buffer and so recovering the eye space Z value required a slightly different method compared to the steps required for the logarithmic depth encoding that the r2 package uses. For historical reasons and for completeness, the method to reconstruct an eye space Z value from a traditional screen space depth value is given in the section on screen space depth encoding.
Recovering Eye space Z (Logarithmic depth encoding)
The r2 package uses a logarithmic depth buffer. Depth values sampled from any depth buffer produced by the package can be transformed to a negated eye space Z value by with a simple decoding equation.
Recovering Eye space Z (Screen space depth encoding)
Note: This section is for completeness and historical interest. Please skip ahead to the section on eye space position reconstruction if you are not interested.
Assuming a screen space depth value screen_depth sampled from the depth buffer at (screen_uv_x, screen_uv_y), it's now necessary to transform the depth value back into normalized-device space. In OpenGL, screen space depth values are in the range [0, 1] by default, with 0 representing the near plane and 1 representing the far plane. However, in OpenGL, normalized-device space coordinates are in the range [(-1, -1, -1), (1, 1, 1)]. The transformation from screen space to normalized-device space is given by:
module ScreenDepthToNDC where screen_depth_to_ndc :: Float -> Float screen_depth_to_ndc screen_depth = (screen_depth * 2.0) - 1.0
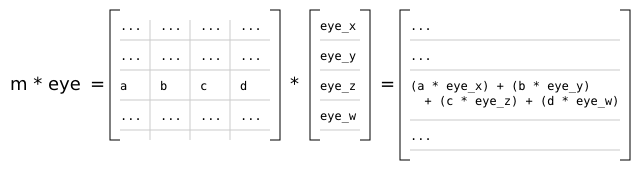
In order to understand how to calculate the eye space depth value from the resulting NDC Z value ndc_z = screen_depth_to_ndc screen_depth, it's necessary to understand how the normalized-device coordinates of f were derived in the first place. Given a standard 4x4 projection matrix m and an eye space position eye, clip space coordinates are calculated by Matrix4x4f.mult_v m eye. This means that the z component of the resulting clip space coordinates is given by:
module ClipSpaceZLong where
import qualified Matrix4f as M4x4;
import qualified Vector4f as V4;
clip_z_long :: M4x4.T -> V4.T -> Float
clip_z_long m eye =
let
m20 = M4x4.row_column m (2, 0)
m21 = M4x4.row_column m (2, 1)
m22 = M4x4.row_column m (2, 2)
m23 = M4x4.row_column m (2, 3)
k0 = (V4.x eye) * m20
k1 = (V4.y eye) * m21
k2 = (V4.z eye) * m22
k3 = (V4.w eye) * m23
in
k0 + k1 + k2 + k3
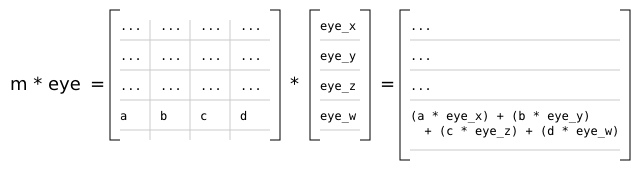
Similarly, the w component of the resulting clip space coordinates is given by:
module ClipSpaceWLong where
import qualified Matrix4f as M4x4;
import qualified Vector4f as V4;
clip_w_long :: M4x4.T -> V4.T -> Float
clip_w_long m eye =
let
m30 = M4x4.row_column m (3, 0)
m31 = M4x4.row_column m (3, 1)
m32 = M4x4.row_column m (3, 2)
m33 = M4x4.row_column m (3, 3)
k0 = (V4.x eye) * m30
k1 = (V4.y eye) * m31
k2 = (V4.z eye) * m32
k3 = (V4.w eye) * m33
in
k0 + k1 + k2 + k3
However, in the perspective and orthographic projections provided by the r2 package, Matrix4x4f.row_column m (2, 0) == 0, Matrix4x4f.row_column m (2, 1) == 0, Matrix4x4f.row_column m (3, 0) == 0, and Matrix4x4f.row_column m (3, 1) == 0. Additionally, the w component of all eye space coordinates is 1. With these assumptions, the previous definitions simplify to:
module ClipSpaceZSimple where
import qualified Matrix4f as M4x4;
import qualified Vector4f as V4;
clip_z_simple :: M4x4.T -> V4.T -> Float
clip_z_simple m eye =
let
m22 = M4x4.row_column m (2, 2)
m23 = M4x4.row_column m (2, 3)
in
((V4.z eye) * m22) + m23
module ClipSpaceWSimple where
import qualified Matrix4f as M4x4;
import qualified Vector4f as V4;
clip_w_simple :: M4x4.T -> V4.T -> Float
clip_w_simple m eye =
let
m32 = M4x4.row_column m (3, 2)
m33 = M4x4.row_column m (3, 3)
in
((V4.z eye) * m32) + m33
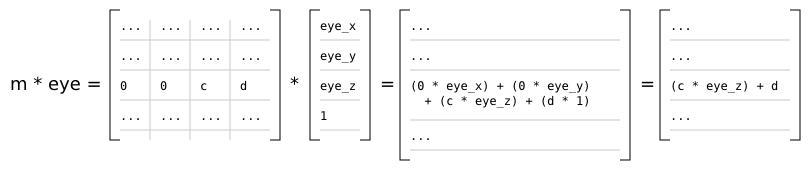
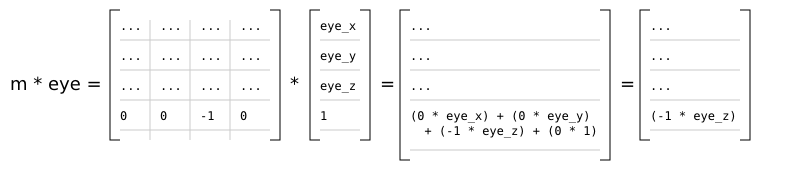
It should be noted that for perspective matrices in the r2 package, Matrix4x4f.row_column m (3, 2) == -1 and Matrix4x4f.row_column m (3, 3) == 0:
This means that the w component of the resulting clip space coordinates is equal to the negated (and therefore positive) eye space z of the original coordinates.
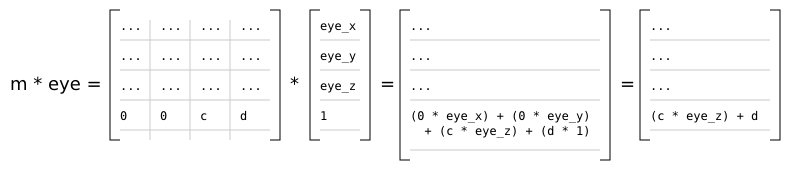
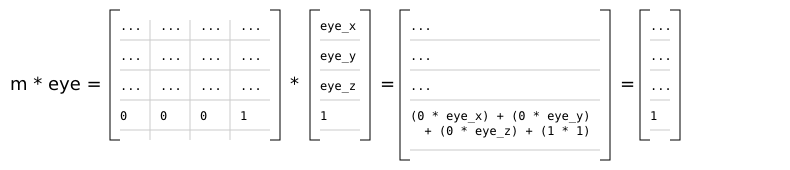
For orthographic projections in the r2 package, Matrix4x4f.row_column m (3, 2) == 0 and Matrix4x4f.row_column m (3, 3) == 1:
This means that the w component of the resulting clip space coordinates is always equal to 1.
As stated previously, normalized-device space coordinates are calculated by dividing a set of clip space coordinates by their own w component. So, given clip_z = ClipSpaceZSimple.clip_z_simple m eye and clip_w = ClipSpaceWSimple.clip_w_simple m eye for some arbitrary projection matrix m and eye space position eye, the normalized-device space Z coordinate is given by ndc_z = clip_z / clip_w. Rearranging the definitions of clip_z and clip_w algebraically yields an equation that takes an arbitrary projection matrix m and a normalized-device space Z value ndc_z and returns an eye space Z value:
module EyeSpaceZ where
import qualified Matrix4f as M4x4;
eye_z :: M4x4.T -> Float -> Float
eye_z m ndc_z =
let
m22 = M4x4.row_column m (2, 2)
m23 = M4x4.row_column m (2, 3)
m32 = M4x4.row_column m (3, 2)
m33 = M4x4.row_column m (3, 3)
a = (ndc_z * m33) - m32
b = (ndc_z * m23) - m22
in
- (a / b)
Recovering Eye space Position
Given that the eye space Z value is known, it's now necessary to reconstruct the full eye space position surface_eye of the surface that resulted in f.
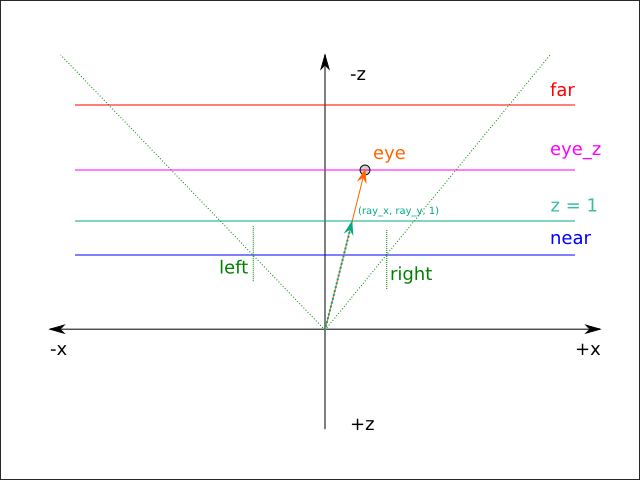
When the current projection is a perspective projection, there is conceptually a ray passing through the near clipping plane ( near) from the origin, oriented towards the eye space position ( eye) of f:
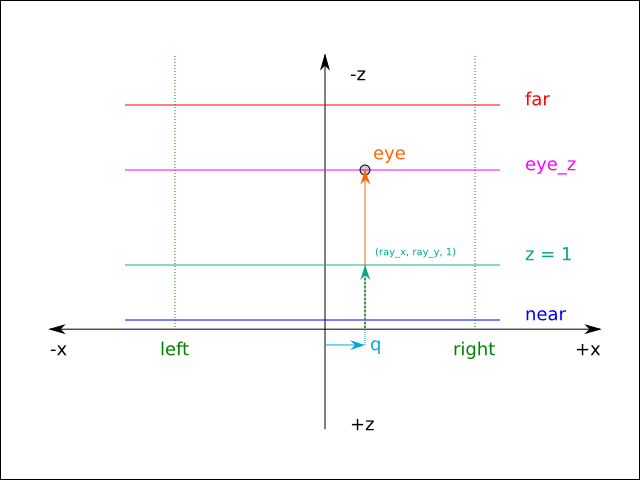
When the current projection is an orthographic projection, the ray is always perpendicular to the clipping planes and is offset by a certain amount ( q) on the X and Y axes:
Assuming ray = Vector3f.V3 ray_x ray_y 1.0, the eye space position of f is given by surface_eye = Vector3f.add3 q (Vector3f.scale ray eye_z). In the case of perspective projections, q = Vector3f.V3 0.0 0.0 0.0. The q term is sometimes referred to as the origin (because q is the origin of the view ray), but that terminology is not used here in order to avoid confusion between the ray origin and the eye space coordinate system origin. It's therefore necessary to calculate q and ray in order to reconstruct the full eye space position of the fragment. The way this is achieved in the r2 package is to calculate q and ray for each of the viewing frustum corners [20] and then bilinearly interpolate between the calculated values during rendering based on screen_uv_x and screen_uv_y.
As stated previously, normalized-device space coordinates are in the range [(-1, -1, -1), (1, 1, 1)]. Stating each of the eight corners of the cube that defines normalized-device space as 4D homogeneous coordinates [22] yields the following values:
module NDCCorners where import qualified Vector4f as V4 near_x0y0 :: V4.T near_x0y0 = V4.V4 (-1.0) (-1.0) (-1.0) 1.0 near_x1y0 :: V4.T near_x1y0 = V4.V4 1.0 (-1.0) (-1.0) 1.0 near_x0y1 :: V4.T near_x0y1 = V4.V4 (-1.0) 1.0 (-1.0) 1.0 near_x1y1 :: V4.T near_x1y1 = V4.V4 1.0 1.0 (-1.0) 1.0 far_x0y0 :: V4.T far_x0y0 = V4.V4 (-1.0) (-1.0) 1.0 1.0 far_x1y0 :: V4.T far_x1y0 = V4.V4 1.0 (-1.0) 1.0 1.0 far_x0y1 :: V4.T far_x0y1 = V4.V4 (-1.0) 1.0 1.0 1.0 far_x1y1 :: V4.T far_x1y1 = V4.V4 1.0 1.0 1.0 1.0
Then, for the four pairs of near/far corners ((near_x0y0, far_x0y0), (near_x1y0, far_x1y0), (near_x0y1, far_x0y1), (near_x1y1, far_x1y1)), a q and ray value is calculated. The ray_and_q function describes the calculation for a given pair of near/far corners:
module RayAndQ where
import qualified Matrix4f as M4x4
import qualified Vector4f as V4
-- | Calculate @(ray, q)@ for the given inverse projection matrix and frustum corners
ray_and_q :: M4x4.T -> (V4.T, V4.T) -> (V4.T, V4.T)
ray_and_q inverse_m (near, far) =
let
-- Unproject the NDC coordinates to eye-space
near_hom = M4x4.mult_v inverse_m near
near_eye = V4.div_s near_hom (V4.w near_hom)
far_hom = M4x4.mult_v inverse_m far
far_eye = V4.div_s far_hom (V4.w far_hom)
-- Calculate a ray with ray.z == 1.0
ray_initial = V4.sub4 far_eye near_eye
ray = V4.div_s ray_initial (V4.z ray_initial)
-- Subtract the scaled ray from the near corner to calculate q
q = V4.sub4 near_eye (V4.scale ray (V4.z near_eye))
in
(ray, q)
The function takes a matrix representing the inverse of the current projection matrix, and "unprojects" the given near and far frustum corners from normalized-device space to eye space. The desired ray value for the pair of corners is simply the vector that results from subtracting the near corner from the far corner, divided by its own z component. The desired q value is the vector that results from subtracting ray scaled by the z component of the near corner, from the near corner.
Note: The function calculates ray in eye space, but the resulting value will have a non-negative z component. The reason for this is that the resulting ray will be multiplied by the calculated eye space Z value [23] to produce an eye space position. If the z component of ray was negative, the resulting position would have a positive z component.
Calculating the ray and q value for each of the pairs of corners is straightforward:
module RayAndQAll where
import qualified NDCCorners
import qualified RayAndQ
import qualified Matrix4f as M4x4
import qualified Vector4f as V4
data T = T {
q_x0y0 :: V4.T,
q_x1y0 :: V4.T,
q_x0y1 :: V4.T,
q_x1y1 :: V4.T,
ray_x0y0 :: V4.T,
ray_x1y0 :: V4.T,
ray_x0y1 :: V4.T,
ray_x1y1 :: V4.T
} deriving (Eq, Ord, Show)
-- | Calculate all rays and qs for the four pairs of near/far frustum corners
calculate :: M4x4.T -> T
calculate inverse_m =
let
(x0y0_ray, x0y0_q) = RayAndQ.ray_and_q inverse_m (NDCCorners.near_x0y0, NDCCorners.far_x0y0)
(x1y0_ray, x1y0_q) = RayAndQ.ray_and_q inverse_m (NDCCorners.near_x1y0, NDCCorners.far_x1y0)
(x0y1_ray, x0y1_q) = RayAndQ.ray_and_q inverse_m (NDCCorners.near_x0y1, NDCCorners.far_x0y1)
(x1y1_ray, x1y1_q) = RayAndQ.ray_and_q inverse_m (NDCCorners.near_x1y1, NDCCorners.far_x1y1)
in
T {
q_x0y0 = x0y0_q,
q_x1y0 = x1y0_q,
q_x0y1 = x0y1_q,
q_x1y1 = x1y1_q,
ray_x0y0 = x0y0_ray,
ray_x1y0 = x1y0_ray,
ray_x0y1 = x0y1_ray,
ray_x1y1 = x1y1_ray
}
Then, by reusing the position = (screen_uv_x, screen_uv_y) values calculated during the initial eye space Z calculation, determining ray and q for the current fragment involves simply bilinearly interpolating between the precalculated values above. Bilinear interpolation between four vectors is defined as:
module Bilinear4 where
import qualified Vector2f as V2
import qualified Vector4f as V4
interpolate :: (V4.T, V4.T, V4.T, V4.T) -> V2.T -> V4.T
interpolate (x0y0, x1y0, x0y1, x1y1) position =
let u0 = V4.interpolate x0y0 (V2.x position) x1y0
u1 = V4.interpolate x0y1 (V2.x position) x1y1
in V4.interpolate u0 (V2.y position) u1
Finally, now that all of the required components are known, the eye space position surface_eye of f is calculated as surface_eye = Vector3f.add3 q (Vector3f.scale ray eye_z).
Implementation
In the r2 package, the R2ViewRays class precalculates the rays and q values for each of the current frustum corners, and the results of which are cached and re-used based on the current projection each time the scene is rendered.
The actual position reconstruction is performed in a fragment shader, producing an eye space Z value using the GLSL functions in R2LogDepth.h and the final position in R2PositionReconstruction.h:
#ifndef R2_LOG_DEPTH_H
#define R2_LOG_DEPTH_H
/// \file R2LogDepth.h
/// \brief Logarithmic depth functions.
///
/// Prepare an eye-space Z value for encoding. See R2_logDepthEncodePartial.
///
/// @param z An eye-space Z value
/// @return The prepared value
///
float
R2_logDepthPrepareEyeZ(
const float z)
{
return 1.0 + (-z);
}
///
/// Partially encode the given _positive_ eye-space Z value. This partial encoding
/// can be used when performing part of the encoding in a vertex shader
/// and the rest in a fragment shader (for efficiency reasons) - See R2_logDepthPrepareEyeZ.
///
/// @param z An eye-space Z value
/// @param depth_coefficient The depth coefficient used to encode \a z
///
/// @return The encoded depth
///
float
R2_logDepthEncodePartial(
const float z,
const float depth_coefficient)
{
float half_co = depth_coefficient * 0.5;
float clamp_z = max (0.000001, z);
return log2 (clamp_z) * half_co;
}
///
/// Fully encode the given eye-space Z value.
///
/// @param z An eye-space Z value
/// @param depth_coefficient The depth coefficient used to encode \a z
/// @return The fully encoded depth
///
float
R2_logDepthEncodeFull(
const float z,
const float depth_coefficient)
{
float half_co = depth_coefficient * 0.5;
float clamp_z = max (0.000001, z + 1.0);
return log2 (clamp_z) * half_co;
}
///
/// Decode a depth value that was encoded with the given depth coefficient.
/// Note that in most cases, this will yield a _positive_ eye-space Z value,
/// and must be negated to yield a conventional negative eye-space Z value.
///
/// @param z The depth value
/// @param depth_coefficient The coefficient used during encoding
///
/// @return The original (positive) eye-space Z value
///
float
R2_logDepthDecode(
const float z,
const float depth_coefficient)
{
float half_co = depth_coefficient * 0.5;
float exponent = z / half_co;
return pow (2.0, exponent) - 1.0;
}
#endif // R2_LOG_DEPTH_H
#ifndef R2_POSITION_RECONSTRUCTION_H
#define R2_POSITION_RECONSTRUCTION_H
/// \file R2PositionReconstruction.h
/// \brief Functions for performing position reconstruction during deferred rendering.
#include "R2Bilinear.h"
#include "R2ViewRays.h"
///
/// Reconstruct an eye-space position from the given parameters.
///
/// @param eye_z The eye-space Z value of the position
/// @param uv The current position on the screen in UV coordinates
/// @param view_rays The current set of view rays
///
vec4
R2_positionReconstructFromEyeZ(
const float eye_z,
const vec2 uv,
const R2_view_rays_t view_rays)
{
vec3 origin =
R2_bilinearInterpolate3(
view_rays.origin_x0y0,
view_rays.origin_x1y0,
view_rays.origin_x0y1,
view_rays.origin_x1y1,
uv
);
vec3 ray_normal =
R2_bilinearInterpolate3(
view_rays.ray_x0y0,
view_rays.ray_x1y0,
view_rays.ray_x0y1,
view_rays.ray_x1y1,
uv
);
vec3 ray =
(ray_normal * eye_z) + origin;
return vec4 (ray, 1.0);
}
#endif // R2_POSITION_RECONSTRUCTION_H
The precalculated view ray vectors are passed to the fragment shader in a value of type R2_view_rays_t:
#ifndef R2_VIEW_RAYS_H
#define R2_VIEW_RAYS_H
/// \file R2ViewRays.h
/// \brief View ray types
/// The type of view rays used to reconstruct positions during deferred rendering.
struct R2_view_rays_t {
/// The bottom left origin
vec3 origin_x0y0;
/// The bottom right origin
vec3 origin_x1y0;
/// The top left origin
vec3 origin_x0y1;
/// The top right origin
vec3 origin_x1y1;
/// The view ray pointing out of the bottom left origin
vec3 ray_x0y0;
/// The view ray pointing out of the bottom right origin
vec3 ray_x1y0;
/// The view ray pointing out of the top left origin
vec3 ray_x0y1;
/// The view ray pointing out of the top right origin
vec3 ray_x1y1;
};
#endif // R2_VIEW_RAYS_H
[20]
This step is performed once on the CPU and is only repeated when the projection matrix changes [21].
[21]
Which, for many applications, may be once for the entire lifetime of the program.
[22]
By simply setting the w component to 1.
[23]
Which is guaranteed to be negative, as only a negative Z value could have resulted in a visible fragment in the geometry buffer.