Logarithmic Depth
Overview
The r2 package exclusively utilizes a so-called logarithmic depth buffer for all rendering operations.
OpenGL Depth Issues
By default, OpenGL (effectively) stores a depth value proportional to the reciprocal of the z component of the clip space coordinates of each vertex projected onto the screen [25]. Informally, the perspective projection matrix used to transform eye space coordinates to clip space will place the negated z component of the original eye space coordinates into the w component of the resulting clip space coordinates. When the hardware performs the division by w to produce normalized-device space coordinates, the resulting z component falls within the range [-1.0, 1.0] (although any point with a z component less than 0 will be clipped away by the clipping hardware). This final value is linearly mapped to a configurable range (typically [0.0, 1.0]) to produce a screen space depth value.
Unfortunately, the encoding scheme above means that most of the depth buffer is essentially wasted. The above scheme will give excessive precision for objects close to the viewing plane, and almost none for objects further away. Fortunately, a better encoding scheme known as logarithmic depth [26] can be implemented that provides vastly greater precision and coexists happily with the standard projection matrices used in OpenGL-based renderers.
Logarithmic Encoding
A logarithmic depth value is produced by encoding a negated (and therefore positive) eye space z value in the manner specified by encode LogDepth.hs:
module LogDepth where
newtype LogDepth =
LogDepth Float
deriving (Eq, Ord, Show)
type Depth = Float
log2 :: Float -> Float
log2 = logBase 2.0
depth_coefficient :: Float -> Float
depth_coefficient far = 2.0 / log2 (far + 1.0)
encode :: Float -> Depth -> LogDepth
encode depth_co depth =
let hco = depth_co * 0.5 in
LogDepth $ log2 (depth + 1.0) * hco
decode :: Float -> LogDepth -> Depth
decode depth_co (LogDepth depth) =
let hco = depth_co * 0.5 in
(2.0 ** (depth / hco)) - 1
The function is parameterized by a so-called depth coefficient that is derived from the far plane distance as shown by depth_coefficient.
The inverse of encode is decode, such that for a given negated eye space z, z = decode d (encode d z).
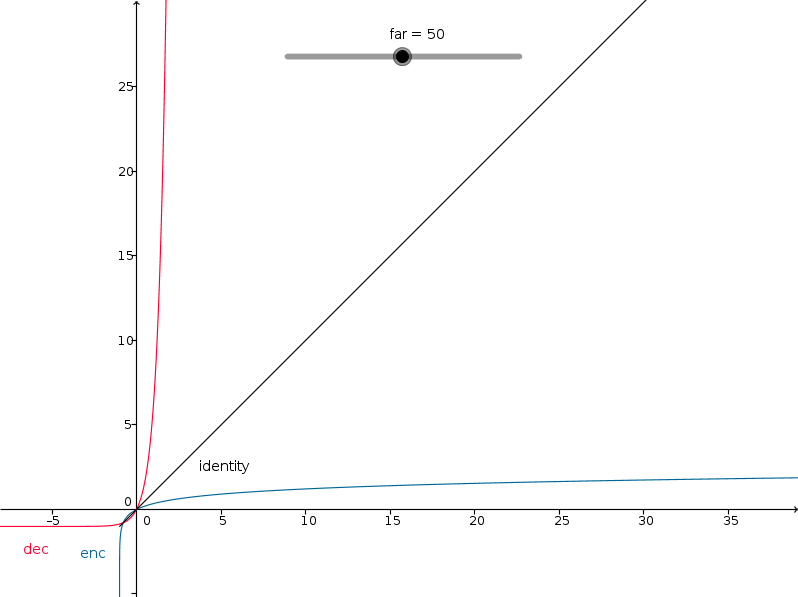
A graph of the functions is as follows:
An interactive GeoGebra construction is provided in log_depth.ggb.
The r2 package uses a slightly modified version of the encoding function that clamps the original z value to the range [0.000001, ∞]. The reason for this is that log2 (0) is undefined, and so attempting to derive a depth value in this manner tends to cause issues with triangle clipping. The encoding function is also separated into two parts as a simple optimization: The encoding function contains a term z + 1.0, and this term can be calculated by a vertex shader and interpolated. The actual functions as implemented are given by R2LogDepth.h:
#ifndef R2_LOG_DEPTH_H
#define R2_LOG_DEPTH_H
/// \file R2LogDepth.h
/// \brief Logarithmic depth functions.
///
/// Prepare an eye-space Z value for encoding. See R2_logDepthEncodePartial.
///
/// @param z An eye-space Z value
/// @return The prepared value
///
float
R2_logDepthPrepareEyeZ(
const float z)
{
return 1.0 + (-z);
}
///
/// Partially encode the given _positive_ eye-space Z value. This partial encoding
/// can be used when performing part of the encoding in a vertex shader
/// and the rest in a fragment shader (for efficiency reasons) - See R2_logDepthPrepareEyeZ.
///
/// @param z An eye-space Z value
/// @param depth_coefficient The depth coefficient used to encode \a z
///
/// @return The encoded depth
///
float
R2_logDepthEncodePartial(
const float z,
const float depth_coefficient)
{
float half_co = depth_coefficient * 0.5;
float clamp_z = max (0.000001, z);
return log2 (clamp_z) * half_co;
}
///
/// Fully encode the given eye-space Z value.
///
/// @param z An eye-space Z value
/// @param depth_coefficient The depth coefficient used to encode \a z
/// @return The fully encoded depth
///
float
R2_logDepthEncodeFull(
const float z,
const float depth_coefficient)
{
float half_co = depth_coefficient * 0.5;
float clamp_z = max (0.000001, z + 1.0);
return log2 (clamp_z) * half_co;
}
///
/// Decode a depth value that was encoded with the given depth coefficient.
/// Note that in most cases, this will yield a _positive_ eye-space Z value,
/// and must be negated to yield a conventional negative eye-space Z value.
///
/// @param z The depth value
/// @param depth_coefficient The coefficient used during encoding
///
/// @return The original (positive) eye-space Z value
///
float
R2_logDepthDecode(
const float z,
const float depth_coefficient)
{
float half_co = depth_coefficient * 0.5;
float exponent = z / half_co;
return pow (2.0, exponent) - 1.0;
}
#endif // R2_LOG_DEPTH_H
A fragment shader can use encode_full to compute a logarithmic depth value from a given positive eye space z value. Alternatively, a vertex shader can compute the z + 1.0 term r from a non-negated eye space z value, and pass r to a cooperating fragment shader which then finishes the computation by applying encode_partial to r. When performing position reconstruction during deferred rendering, the original eye space z value of a fragment is retrieved by negating the result of decode applied to a given logarithmic depth sample.
The original derivation of the encoding and decoding functions as described by Brano Kemen used the w component of the resulting clip space coordinates. Unfortunately, this does not work correctly with orthographic projections, as the typical orthographic projection matrix will produce clip space coordinates with a w component always equal to 1. Aside from the effects that this will have on depth testing (essentially mapping the depth of all fragments to the far plane), it also makes position reconstruction impossible as the original eye space z value cannot be recovered. Instead, the r2 package uses the negated eye space z value directly in all cases.